【二叉树】【数据结构】【buu】[GUET-CTF2019]number_game

【二叉树】

参考链接：

[详细图解二叉树四种遍历(前序中序后序层次遍历)]https://blog.csdn.net/m0_68681879/article/details/127847415?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522172170617216800178534776%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=172170617216800178534776&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-127847415-null-null.142

[二叉树遍历的实现（超详细解析，小白必看系列）]https://blog.csdn.net/weixin_45031801/article/details/133747485?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522172171563016800182746442%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=172171563016800182746442&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-3-133747485-null-null.142

[数据结构——顺序队列与链式队列的实现]https://blog.csdn.net/m0_74712453/article/details/135351817?spm=1001.2014.3001.5502

[数据结构——二叉树四种遍历的实现]https://blog.csdn.net/m0_74712453/article/details/135360309?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522172171563016800182746442%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=172171563016800182746442&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduend~default-1-135360309-null-null.142

[东哥带你刷二叉树（纲领篇）]https://labuladong.online/algo/essential-technique/binary-tree-summary/

正文

一、树的概念

1、树的定义

1）树
树是 n(n≥0) 个结点的有限集合。当 n>0 时，它是一棵非空树，满足如下条件：
1）有且仅有一个特定的结点，称为根结点Root；
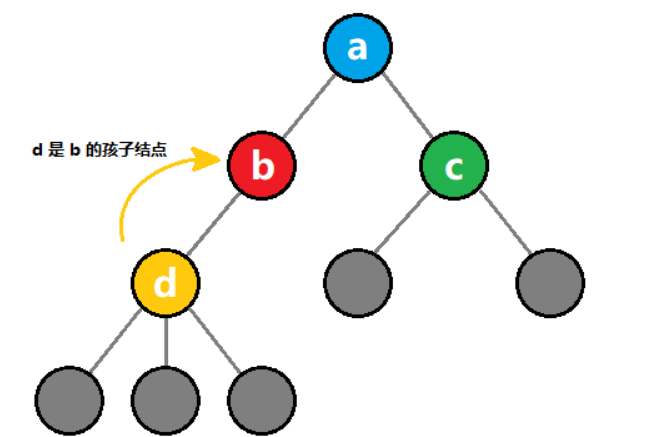
2）除根结点外，其余结点分为 m 个互不相交的有限集合 T1、T2、…………、Tm，其中每一个 Ti(1≤i≤m) 又是一棵树，并且为根结点 Root 的子树。如图所示，代表的是一棵以 a 为根结点的树。

tree

2）空树
当 n=0，也就是 0 个结点的情况也是树，它被称为空树。

3）子树
树的定义用到了递归的思想。即树的定义中还是用到了树的概念，如图所示，T1 和 T2 就是结点 a 的子树。结点 d、g、h、i 组成的树又是结点 b 的子树等等。

kidTree

子树的个数没有限制，但是它们一定是互不相交的，如下图所示的就不是树。因为在这两个图中，a 的子树都有相交的边。

notTree

2、结点的定义

树的结点包含一个数据域和 m 个指针域用来指向它的子树。结点的种类分为：根结点、叶子结点、内部结点。结点拥有子树的个数被称为结点的度。树中各个结点度的最大值被称为树的度。

1）根结点
一棵树的根结点只有一个。

2）叶子结点
度为 0 的结点被称为叶子结点或者终端结点。叶子结点的不指向任何子树。

3）内部结点
除了根结点和叶子结点以外的结点，被称为内部结点。

points

如上图所示，红色结点为根结点，蓝色结点为内部结点，黄色结点为叶子结点。

3、结点间关系
1）孩子结点
对于某个结点，它的子树的根结点，被称为该结点的孩子结点。

chilTree

如上图所示，黄色结点 d 是红色结点 b 的孩子结点。

2）父结点
而该结点被称为孩子结点的父结点。

faTree

如上图所示，蓝色结点 a 是红色结点 b 的父结点。

3）兄弟结点
同一父结点下的孩子结点，互相称为兄弟结点。

broTree

如上图所示，绿色结点 c 和红色结点 b 互为兄弟结点。

4、树的深度
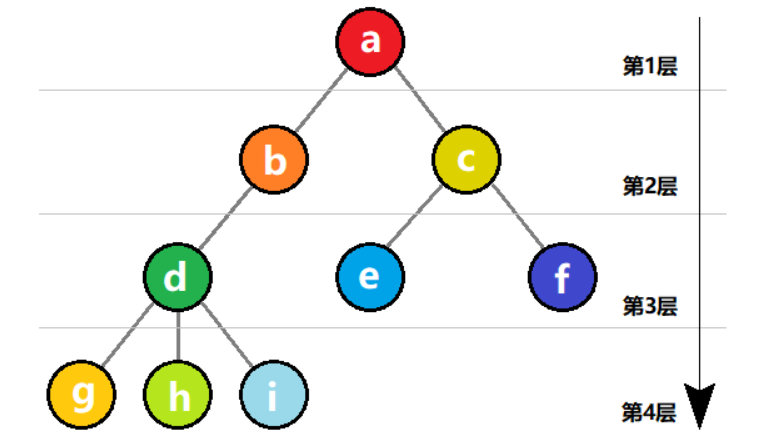
结点的层次从根结点开始记为第 1 层，如果某结点在第 i 层，则它的子树的根结点就在第i+1 层，树中结点的最大层次称为树的深度。
如下图所示，代表的是一棵深度为 4 的树。

treeDeepth

5、森林的定义
森林是 m 棵互不相交的树的集合，对于树的每个结点而言，其子树集合就是森林。
如图所示，b 和 c 两棵子树组成的集合就是一个森林。

forest

二、二叉树的概念
1、二叉树的性质
二叉树是一种树，它有如下几个特征：
1）每个结点最多 2 棵子树，即每个结点的孩子结点个数为 0、1、2；
2）这两棵子树是有顺序的，分别叫：左子树和右子树；
3）如果只有一棵子树的情况，也需要区分顺序，如图所示：

b 为 a 的左子树；

leftKidTree

c 为 a 的右子树；、

righjtKidTree

2、特殊二叉树
1）斜树
所有结点都只有左子树的二叉树被称为左斜树。

leftTree

所有结点都只有右子树的二叉树被称为右斜树。

rightTree

斜树有点类似线性表，所以线性表可以理解为一种特殊形式的树。

2）满二叉树
对于一棵二叉树，如果它的所有根结点和内部结点都存在左右子树，且所有叶子结点都在同一层，这样的树就是满二叉树。

fullTree

满二叉树有如下几个特点：
1）叶子结点一定在最后一层；
2）非叶子结点的度为 2；
3）深度相同的二叉树，满二叉树的结点个数最多，为（其中 h 代表深度）。

2）完全二叉树
对一棵具有 n 个结点的二叉树按照层序进行编号，如果编号 i 的结点和同样深度的满二叉树中的编号 i 的结点在二叉树中位置完全相同，则被称为完全二叉树。

perfectTree

满二叉树一定是完全二叉树，而完全二叉树则不一定是满二叉树。
完全二叉树有如下几个特点：
1）叶子结点只能出现在最下面两层。
2）最下层的叶子结点一定是集中在左边的连续位置；倒数第二层如果有叶子结点，一定集中在右边的连续位置。
3）如果某个结点度为 1，则只有左子树，即不存在只有右子树的情况。
4）同样结点数的二叉树，完全二叉树的深度最小。

如下图所示，就不是一棵完全二叉树，因为 5 号结点没有右子树，但是 6 号结点是有左子树的，不满足上述第 2 点。

notPErfectTree

3、二叉树的性质

接下来我们来看下，二叉树有哪些重要的性质。

1）性质1
【性质1】二叉树的第 i(i≥1) 层上至多有 2^i-1 个结点。

既然是至多，就只需要考虑满二叉树的情况，对于满二叉树而言，当前层的结点数是上一层的两倍，第一层的结点数为 1，所以第 i 的结点数可以通过等比数列公式计算出来，为2^i-1 。

2）性质2
【性质2】深度为 h 的二叉树至多有 2^h-1结点。

对于任意一个深度为 h 的二叉树，满二叉树的结点数一定是最多的，所以我们可以拿满二叉树进行计算，它的每一层的结点数为1、2、4、8 …、2^h-1。
利用等比数列求和公式，得到总的结点数为：1+2+4+8+ …+2^h-1=2^h-1

3）性质3
【性质3】对于任意一棵二叉树 T，如果叶子结点数为 x0，度为 2 的结点数为 x2，则x0=x2+1

令 x1 代表度为 1 的结点数，总的结点数为 n，则有：n=x0+x1+x2 ……①
任意一个结点到它孩子结点的连线我们称为这棵树的一条边，对于任意一个非空树而言，边数等于结点数减一，令边数为 e，则有：e=n−1 ……②

性质3

对于度为 1 的结点，可以提供 1 条边，如图中的黄色结点；对于度为 2 的结点，可以提供 2 条边，如图中的红色结点。所以边数又可以通过度为 1 和 2 的结点数计算得出：e=x1+2x2 ……③

联立上述①②③三个等式，得到：e=n−1=x0+x1+x2−1=x1+2x2

化简后，得证：x0=x2+1

4）性质4
**【性质4】具有 n 个结点的完全二叉树的深度为 **[log2]n+1

由【性质2】可得，深度为 ℎh 的二叉树至多有2^h-1个结点。所以，假设一棵树的深度为 h，它的结点数为 n，则必然满足：n≤2^h-1

由于是完全二叉树，它一定比深度为 ℎ−1h−1 的结点数要多，即：2^h-1 - 1 < n

将上述两个不等式，稍加整理，得到：2^h-1 ≤ n < 2^h

然后，对不等式两边取以2为底的对数，得到：h-1≤[log2]n+1 <h

这里，由于 h 一定是整数，所以有：h = [log2]n+1

二、二叉树的储存和创建

1、创建二叉链结构

// 二叉树结构体
typedef struct BrinyTree
{
	struct BrinyTree* left;
	struct BrinyTree* right;
	int data;
}BT;

2、手动构建一颗树

其实构建一棵树的思想还是挺简单的，按照图示创建6个节点，并根据图中的样子将节点顺次链接起来

// 创建一个节点 （有返回值，返回值类型为---结构体指针）
BT* BuyNode(int x)
{
	BT* newnode = (BT*)malloc(sizeof(BT));
	if (newnode == NULL)
	{
		perror("malloc fail!");
		exit(-1);
	}
	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;

return newnode;

}

// 创建一个树
BT* CreatBinaryTree()
{
	// 创建6个节点
	BT* node1 = BuyNode(1);
	BT* node2 = BuyNode(2);
	BT* node3 = BuyNode(3);
	BT* node4 = BuyNode(4);
	BT* node5 = BuyNode(5);
	BT* node6 = BuyNode(6);

    //将结点连接起来，构成自己想要的树
    node1->left = node2;
    node1->right = node4;
    node2->left = node3;
    node4->left = node5;
    node4->right = node6;

    return node1;
}

三、二叉树的遍历（重点）

1、前序遍历

前序遍历的代码非常简洁，短短几行即可操作，先看代码：

// 前序遍历 根 左 右
void  PrevOrder(BT* root)
{
	if (root == NULL)
	{
		printf("NULL "); // 如果为空，就打印
		return;      // 当前函数结束
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

前序遍历

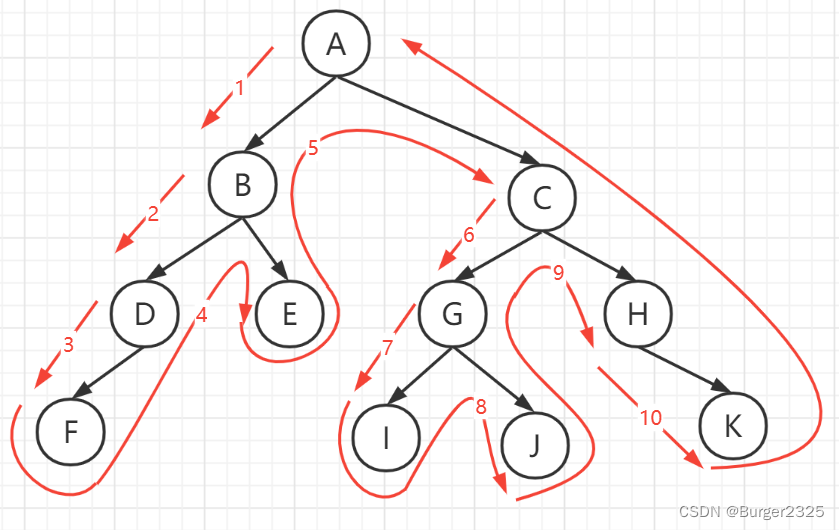
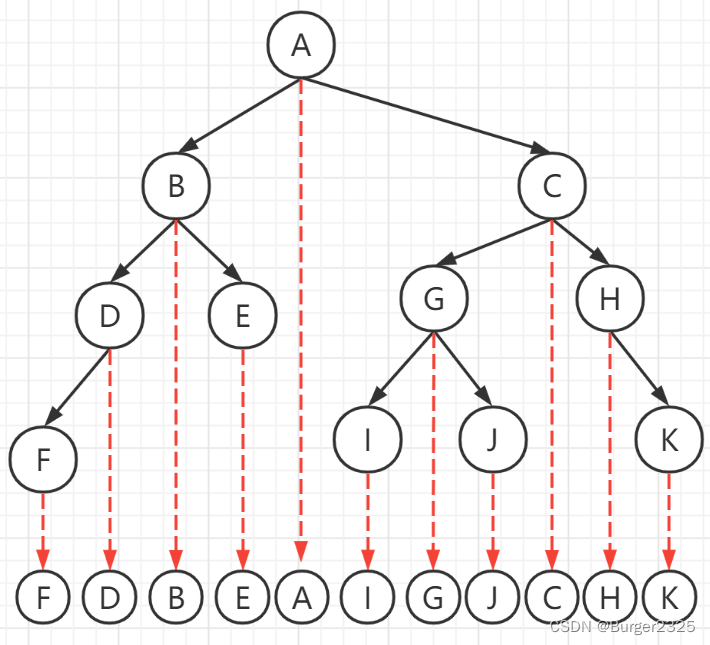
2、中序遍历

中序遍历的代码和前序遍历一样，看起来都非常简洁：

// 中序遍历  左 根 右
void InOrder(BT* root)
{
	if (root == NULL)
	{
		printf("NULL "); // 如果为空，就打印
		return;      // 当前函数结束
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

中序遍历 (2)

3、后序遍历

代码演示：

// 后序 左 右 根
void PosOrder(BT* root)
{
	if (root == NULL)
	{
		printf("NULL "); // 如果为空，就打印
		return;      // 当前函数结束
	}
	PosOrder(root->left);
	PosOrder(root->right);
	printf("%d ", root->data);
}

4、层次遍历

代码演示：

// 初始化队列 
void InitQueue(SqQueue *Q)
{
	Q->front = Q->rear = 0;
}

// 辅助队列的入队操作 
void EnQueue(SqQueue *Q, QElemType q)
{
	if ((Q->rear + 1) % MAXSIZES == Q->front)
		return;
	Q->data[Q->rear] = q;
	Q->rear = (Q->rear + 1) % MAXSIZES;
}
// 辅助队列的出队操作 
void DeQueue(SqQueue *Q, QElemType *q)
{
	if (Q->front == Q->rear)
		return;
	*q = Q->data[Q->front];
	Q->front = (Q->front + 1) % MAXSIZES;
}

void LevelOrder(BiTree T)
{
	SqQueue Q;
	InitQueue(&Q);	// 初始化辅助队列
	BiTree p;
	EnQueue(&Q, T);	// 将根节点入队
	while(Q.front != Q.rear)	// 队列不空则循环 
	{
		DeQueue(&Q, &p);	// 队头结点出队
		printf("%c", p->data);
		if (p->lchild != NULL)
		{
			EnQueue(&Q, p->lchild);	// 左子树不空,则左子树根节点入队 
		}
		if (p->rchild != NULL)
		{
			EnQueue(&Q, p->rchild);	// 右子树不空,则右子树根节点入队 
		} 
	} 
}

[GUET-CTF2019]number_game

下载完拖入010是elf文件，直接拖入64位ida

main

由sub_4006D6可知flag长度为10

sub_400758是用二叉树把flag传给了v4，

先给本身赋值赋值，

然后把左结点来把奇数位进行赋值

右结点把偶数位进行赋值

sub_400807这是个二叉树的中序遍历

中序遍历

sub_400881是吧v7的值输入到特定的地址中

sub_400917是个检查函数，跟进查看

这是个二维数组的检查函数要求在一个5*5的二维数组中每行 or 每列不能有相同的数字

跟进unk_601060并且将它按照5*5的格式展开如下

14#23
30#1#
0#23#
#3##0
42##1

这是个数独游戏，把每个数字写出来之后

按照从上到下，从左到右的顺序排列好后

按照二叉树的中序排列逆回去就是flag